激光在非线性介质中的传播和基于新型激光场的非线性调控是当前非线性物理研究的两大前沿方向。通过改变色散、衍射和非线性特性,可有效调控波在非线性介质中的传播特性,也为研究其中的新现象和物理效应开辟了新途径。相比凝聚态和固体物理,玻色-爱因斯坦凝聚为研究诸多非线性现象提供了更为干净和高度可控的媒介,如平均场近似下的亮、暗孤子和多体物理。为了获得稳定的孤子解,通常采用三种方法:由相向传播的激光束形成的光晶格(线性调控),费希巴赫共振产生的非线性调控,以及通过激光实现缀饰原子自旋态产生的自旋轨道耦合效应。
今年初,西安光机所瞬态光学与光子技术国家重点实验室阿秒科学技术研究方向曾健华副研究员(中国科学院青促会会员)团队在上述两大非线性物理前沿理论研究方面取得系列创新成果,相继发表在Nature子刊《Communications Physics》和3篇中科院二区物理期刊上(《Annalen der Physik》、《Frontiers of Physics》、《Commun. Nonlinear Sci. Numer. Simulat.》)。
上世纪六十年代激光诞生不久之后,诺贝尔物理学奖获得者Townes在其奠基性理论文章中指出“激光在二维自聚焦非线性介质中难以实现稳定传播,会发生临界塌缩”,后人称此现象为“Townes孤子”。之后,克服激光传播的临界塌缩现象是物理以及其它领域科学家孜孜以求的目标。非线性光学领域通常采用的方法是引入线性周期势(如光子晶体)和竞争自聚焦三阶-自散焦五阶非线性,然而通过调节光场的衍射和三五阶竞争非线性来克服塌缩现象仍处于研究萌芽阶段。曾健华团队在此前非线性调控研究 [Phys. Rev. A 85, 023824 (2012); Phys. Rev. E 85, 047601 (2012), 86, 036607 (2012), 88, 025201 (2013), 95, 052214 (2017) ],和近期线性-非线性调控研究[Adv. Photonics 1, 046004 (2019); Opt. Lett. 44, 1206 (2019), 44, 2661 (2019); Non. Dynamics 98,985(2019) ]的基础上,通过结合线性周期势和竞争三五阶非线性特性,理论研究了激光在分数衍射介质中的传播特性,发现了三类局域于能带中且能稳定传播的二维局域孤子解,包括基模、带隙涡旋和类截断非线性布洛赫波(孤子簇),从而克服了二维自聚焦介质中的临界塌缩现象。2020年1月该结果《Preventing critical collapse of higher-order solitons by tailoring unconventional optical diffraction and nonlinearities》发表在Nature子刊《Communications Physics》上(https://www.nature.com/articles/s42005-020-0291-9)。
图1. 二维空间中的涡旋帯隙孤子(四模束缚态)的俯视结构图(上行)、相位图(中行)及其特征值(下行)。[ Commun. Phys. 3, 26 (2020)]
上述工作第一作者为西安光机所和国科大17级博士生曾亮维;至此曾亮维同学已经以第一作者发表6篇学术论文(含 Adv. Photonics, Non. Dynamics, JOSA-B各1篇和Opt. Lett. 2篇)。
同时,针对激光在纯非线性饱和介质中同步调控光衍射和自聚焦非线性这一尚未研究的科学问题,今年该团队的理论研究结果《1D Solitons in Saturable Nonlinear Media with Space Fractional Derivatives》发表在《Annalen der Physik》(https://doi.org/10.1002/andp.201900385)上。文章首次采用纯非线性调控方法研究了衍射可调控的饱和非线性介质中激光的传播特性,发现在三阶或五阶自聚焦非线性作用下,均存在稳定的基模孤子和高阶结构(同相位双峰结构和反相位偶极子);首次找到局域于非线性晶格单周期内的稳定偶极孤子模。同时,题目为《Self-trapped spatially localized states in combined linear-nonlinear periodic potentials》的理论工作结果发表在《Frontiers of Physics》(https://doi.org/10.1007/s11467-019-0930-3)。文章通过线性-非线性调控手段,研究了一维和二维自聚焦非线性光学或物质波介质中的局域波特性,发现了两类自捕获空间局域带隙模(带隙孤子和截断非线性布洛赫波)。研究亮点是可以克服上面提到的二维自聚焦存在的临界塌缩现象,空间局域模的稳定性同时具有线性和非线性周期势独特的优势。这两篇论文的第一作者均为博士研究生石金城。
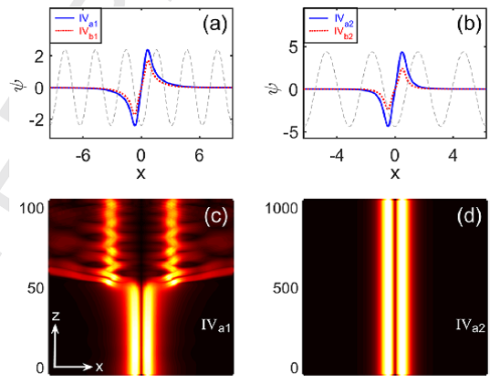
图2. 饱和非线性介质中局域于非线性晶格单周期内的一维偶极孤子(上图)及其传播动力学(下图)。[Annalen der Physik 532, 190085(2020)]
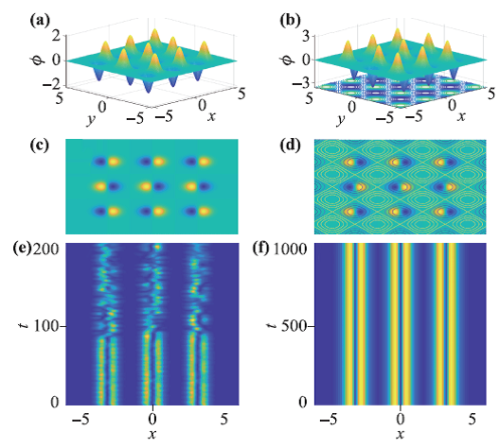
图3. 耦合线性-非线性周期势中的二维截断非线性布洛赫波立体图(上行)、俯视图(中行)及其动力学演化图(下行)。[Front. Phys. 15, 12607(2020)]
此外,在含自旋-轨道耦合效应的玻色-爱因斯坦凝聚的纯非线性调控方面,团队的研究成果《One-dimensional localized modes of spin-orbit-coupled Bose-Einstein condensates with spatially periodic modulated atom-atom interactions: Nonlinear lattices》发表在《Commun. Nonlinear Sci. Numer. Simulat.》(https://doi.org/10.1016/j.cnsns.2020.105217)。文章首次在双分量自旋-轨道耦合玻色-爱因斯坦凝聚中引入非线性空间周期性调控手段,从理论和计算方面研究了两类局域模:基本孤子和孤子对(偶极子和双峰孤子)的存在和稳定情况,探讨了系统化学势、自旋轨道耦合和原子相互作用强度对局域模的影响,发现只有当原子相互作用和凝聚体相互作用都为自聚焦时才存在稳定解。论文第一作者为博士研究生陈俊波。
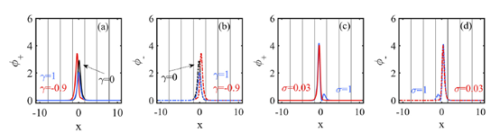
图4. 具有空间周期性调制原子-原子相互作用的自旋-轨道耦合玻色-爱因斯坦凝聚在不同交叉相互作用(a,b)和自旋-轨道耦合系数(c,d)下的一维基态模形状。自旋向上(a,c)和自旋向下组分波函数(b,d)。[Commun. Nonlinear Sci. Numer. Simulat. 85, 105217(2020)]
以上研究工作得到了国家自然科学基金和中国科学院青年创新促进会的支持。(瞬态室 供稿)






 陕公网安备 61019002000980号
陕公网安备 61019002000980号